一、什么是树
树是一种分层数据的抽象模型。
二、树的相关术语
一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点(除了顶部的第一个节点)以及零个或者多个子节点。
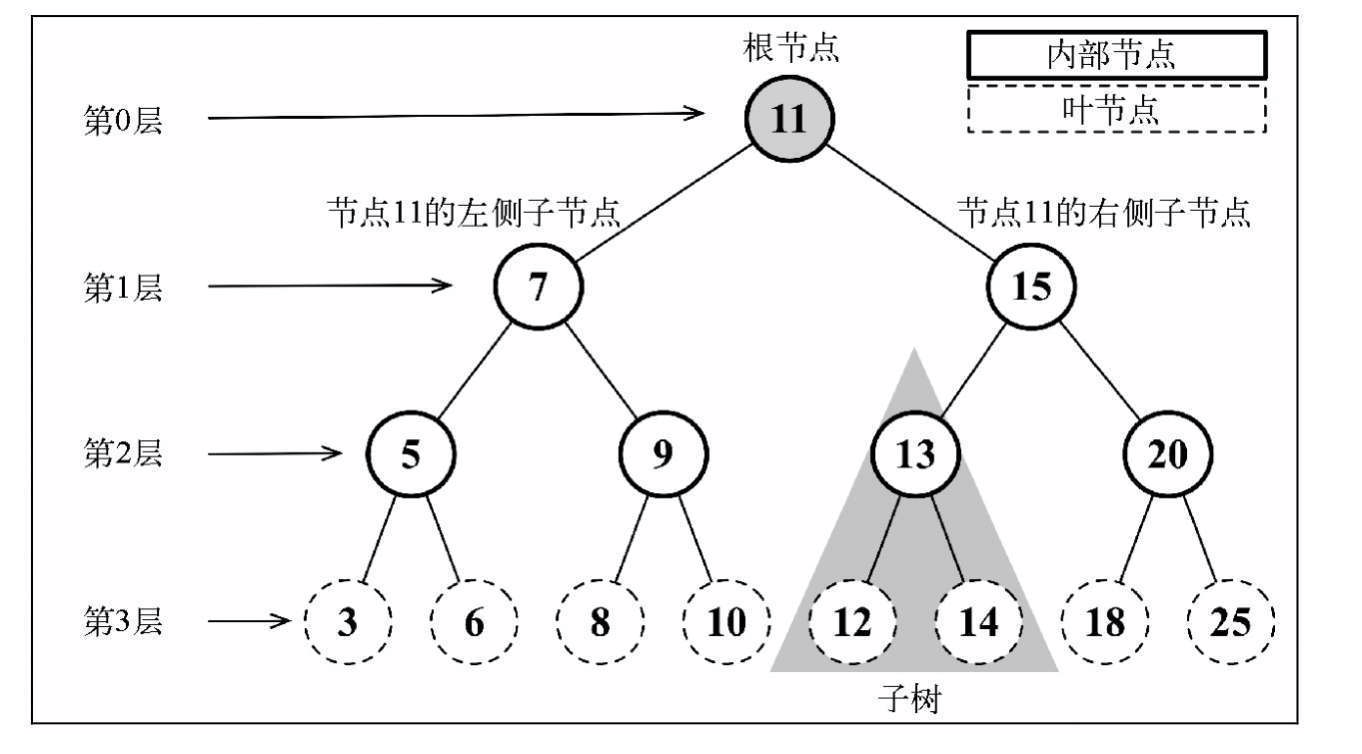
- 根节点:位于树顶部的节点,根节点没有父节点。
- 内部节点: 至少有一个子节点的节点
- 外部节点(叶节点):没有子节点的节点
- 子树: 子树由节点和它的后代组成
- 深度:节点的深度取决于它的祖先节点的数量。如节点3的祖先节点数量为3,它的深度为3
三、二叉树和二叉搜索树
-
二叉树
二叉树中的节点只能有两个子节点,一个是左侧子节点,另一个是右侧子节点。
-
二叉搜索树
二叉搜索树(BST)是二叉树的一种,但是只允许在左侧子节点存储比父节点小的值,在右侧节点存储比父节点大的值。
-
代码实现一棵二叉搜索树
// 创建Node类来表示二叉搜索树中的节点
class Node {
constructor(key) {
this.key = key; // 节点值
this.left = null; // 左侧子节点引用
this.right = null; //右侧子节点引用
}
}
// 创建BinarySearchTree来表示一棵二叉搜索树
class BinarySearchTree {
constructor() {
this.root = null; // Node类型的根节点
}
/**
* 在树中插入一个新的节点
*/
insert(key) {
if (this.root == null) {
this.root = new Node(key);
} else {
this.insertNode(this.root,key);
}
}
/**
* 插入节点的递归方法
*/
insertNode(node,key) {
if(key < node.key) {
if(node.left == null) {
node.left = new Node(key);
} else {
this.insertNode(node.left,key);
}
} else {
if(node.right == null) {
node.right = new Node(key);
} else {
this.insertNode(node.right,key);
}
}
}
/**
* 在树中查找一个节点。若节点存在,则返回true,否则返回false
*/
search(key) {
return this.searchNode(this.root,key);
}
/**
* 在树中查找一个节点的递归方法
*/
searchNode(node,key) {
if(node == null) {
return false;
}
if(key < node.key) {
return this.searchNode(node.left,key);
} else if(key > node.key) {
return this.searchNode(node.right,key);
} else {
return true;
}
}
/**
* 中序遍历树中全部节点
*/
inOrderTraverse(callback) {
this.inOrderTraverseNode(this.root,callback);
}
/**
* 中序遍历树中全部节点的递归方法
*/
inOrderTraverseNode(node,callback) {
if(node != null) {
this.inOrderTraverseNode(node.left,callback);
callback(node.key)
this.inOrderTraverseNode(node.right,callback);
}
}
/**
* 先序遍历树中全部节点
*/
preOrderTraverse(callback) {
this.preOrderTraverseNode(this.root,callback)
}
/**
* 先序遍历树中全部节点的递归方法
*/
preOrderTraverseNode(node,callback) {
if(node != null) {
callback(node.key);
this.preOrderTraverseNode(node.left,callback);
this.preOrderTraverseNode(node.right,callback);
}
}
/**
* 后续遍历树中全部节点
*/
postOrderTraverse(callback) {
this.postOrderTraverseNode(this.root,callback);
}
/**
* 后续遍历树中全部节点的递归方法
*/
postOrderTraverseNode(node,callback) {
if(node != null) {
this.postOrderTraverseNode(node.right);
this.postOrderTraverseNode(node.left);
callback(node.key);
}
}
/**
* 返回树中最小的几点,实际上是二叉搜索树最左下方的节点
*/
min() {
return this.minNode(this.root);
}
/**
* 找到二叉搜索树中最小节点的递归方法
*/
minNode(node) {
let current = node;
while(current != null && current.left != null) {
current = current.left;
}
return current;
}
/**
* 返回树中最大的值,实际上是二叉搜索树中最右的节点
*/
max() {
return this.maxNode(this.root);
}
/**
* 寻找二叉搜索树中的最大节点的递归方法
*/
maxNode(node) {
let current = node;
while(current != null && current.right != null) {
current = current.right;
}
return current;
}
/**
* 从树中移除某个节点
*/
remover(key) {
this.root = this.removeNode(this.root,key);
}
removeNode(node,key) {
if(node == null) {
return null;
}
if(key < node.key) {
node.left = this.removeNode(node.left,key);
return node;
} else if(key > node.key) {
node.right = this.removeNode(node.right,key);
return node;
} else {
// 直到node.key === key
// 第一种情况,要移除的节点是叶节点
if(node.left == null && node.right == null) {
node = null;
return node;
}
// 第二种情况,要移除的节点只有一个子节点
if(node.left == null) {
node = node.right;
return node;
} else if(node.right == null) {
node.left == null;
return node;
}
// 第三种情况,要移除的节点有两个子节点
const aux = this.minNode(node.right);
node.key = aux.key;
node.right = this.removeNode(node.right,aux.key);
return node;
}
}
}
const binarySearchTree = new BinarySearchTree();
binarySearchTree.insert(11);
binarySearchTree.insert(7);
binarySearchTree.insert(5);
binarySearchTree.insert(3);
const printNode = (value) => console.log(value);
binarySearchTree.inOrderTraverse(printNode); // 3 5 7 11
binarySearchTree.preOrderTraverse(printNode); // 11 7 5 3
console.log(binarySearchTree.min()); // Node { key: 3, left: null, right: null }
console.log(binarySearchTree.search(7)); // true